Q.254. Common area between intersecting circles

Question 254.
Find the common area of two circles of equal radii, R, each passing through the centre of the other.

Answer 254.
Let the circles be drawn in the x-y coordinate plane with their centers at (-R/2, 0) and (R/2, 0) as shown in the figure.

Their equations are
(x + R/2)^2 + y^2 = R^2 ... (1) and
(x - R/2)^2 + Y^2 = R^2 ... (2)

They intersect on the y-axis.
=> Required area
4 times the shaded area
= 4 ∫ (x=0 to R/2) √[R^2 - (x - R/2)^2] dx
= 4 [(x - R/2)/2 * √[R^2 - (x - R/2)^2] + (R^2/2) * arcsin[(x - R/2) / R] ... (x=0 to R/2)
= 4 [ - R/4 * (√3/2) R - (R^2/2) arcsin(-1/2) ]
= (2π/3) R^2 - (√3/2) R^2
= (2π/3 - √3/2) R^2.

Alternate Geometrical Approach:
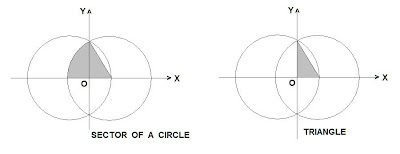
Join the center of the right-hand circle to the point of intersection of the two circles on +ve y-axis.
Refer to the figure.

Base of the triangle = R/2
Height of the triangle = √[R^2 - (R/2)^2] = (√3/2) R
Area of the gtriangle = (1/2) * (R/2) * (√3/2) R = (1/4) * (√3/2) R^2
 Angle subtended by the arc of the circle at gthe center = arccos (R/2) / R = π/6
=> area of the sector of the circle = (π/6) R^2

Required area
= 4 * Shaded area
= 4 * [area of the sector of the circle - area of the right triangle.]
= 4 * [(π/6) R^2 - (1/4) * (√3/2) R^2]
= (2π/3 - √3/2) R^2.

Link to YA!